Energy Content and Electromagnetic Force
The next logical question is what energy can be stored and delivered by the capacitor:
C1.4 ENERGY CONTENTS / FORCE MANIFESTATIONS
C 1.4.1 Energy contents
The energy stored in a capacitor can be described as
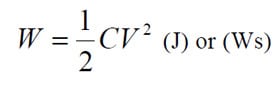
……………[C1-20]
C 1.4.2 Force action
from electromagnetic fields
Parallel current carrying conductors are surrounded by magnetic fields exerting forces on each other. If currents flow in the same direction the fields (and the conductors) attract each other. If the current flows in opposite directions as in the Figure C1-24 they are repelling each other.
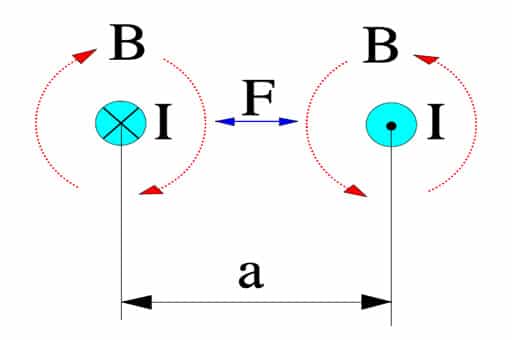
If
- the conductor length l is expressed in m,
- the current I is expressed in A and
- the distance a is expressed in m,
the force per meter between the conductors will be
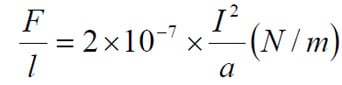
………………………[C1-21]
According to the formula (C1-1) Q = C x V (As). If this expression is derived we obtain dQ/dt = I = C x dV/dt (A).
Pulse loads are not unusual, especially in conditions with high voltage gradients, and thus high charging currents also occur which might cause appreciable magnetic fields between close lead patterns, for example.
C 1.4.3 Force action in electrostatic fields
Capacitors are typical examples of applications where electrostatic fields are applied. These fields can generate significant mechanical forces. If we know the electrode distance d (m) it’s easy to determine the electric field strength E (V/m). Then we can outline the force per unit area, i.e. the pressure that the electrodes exert on the dielectric.
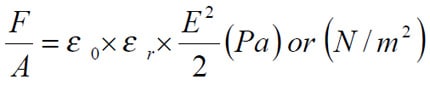
……………………………….. [C1-22]
Example. Suppose we have an oil impregnated paper capacitor with r = 5 and the dielectric = 15 m (0.6 mils) which is loaded with 250VAC. Then the instantaneous maximum pressure will be
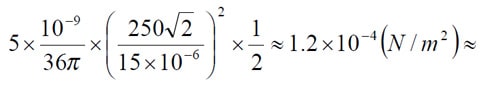
0.1 kp/cm2 !
If we instead calculate on a 35 V solid tantalum capacitor with a typical and approximate dielectric thickness of 0.2 mm (0.008 mils) the formula gives at 30 V DC a pressure of
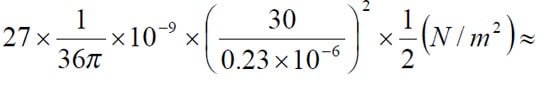
2 N/mm2 !
It is difficult to determine how much the dielectric is influenced by such forces, especially when the electrodes have such complex configurations. Electrostatic action of such forces here is of vital importance.
Electrostatic Force Potential Impact
We learned in the article about the energy stored in the capacitor, but what is also important and demonstrated is that there is enormous mechanical pressure between the electrodes once voltage is applied.
This can be considered in failure analyses if we have a solid, sharp impurity within the capacitor dielectric – it may degrade the insulator not only by inducing electrical conductivity/increasing leakage current, but also causing a mechanical damage to the dielectric due to the high electrostatic pressure between the electrodes. Hard and sharp micro-crystals in amorphous dielectric could be an example of such defects.
